【統計学】～検査前確率、検査後確率～

※2020年９月3日追記　一部に計算間違い（検査後確率9.8%→正しくは0.98%）がありましたので訂正しました。

↓参考資料

スッキリわかる！　臨床統計はじめの一歩　改訂版　羊土社

「検査すれば良いというものではない。検査の使いどころを間違えると役に立たないどころか、偽陽性の人に過剰な治療を行ってしまうなど、むしろ有害な結果を招いてしまう。」
…と書いてあったので、本当かな？と。Excelで数字入れて実際に試してみました。

検査前確率、検査後確率

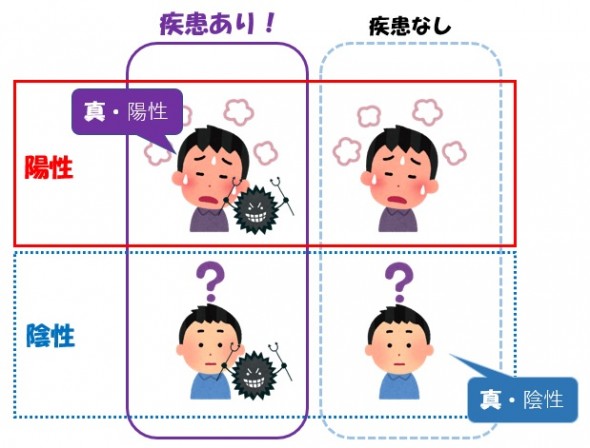
治療者も患者さんも、「陽性だー！治療すべし」「陰性だった、安心だ！」と検査結果に一喜一憂しがち。
だが、検査結果は絶対ではない。偽陽性、偽陰性が生じる。

（実際の感染者数）÷（全体の人数）＝”検査前確率”

（陽性者のうち、実際の感染者数）÷（陽性者の人数）＝”検査後確率”

と呼ばれる。（検査後確率は”陽性的中率”とも言われる。）

例えば、感度99％、特異度99％という超有能な検査を行うとしても、

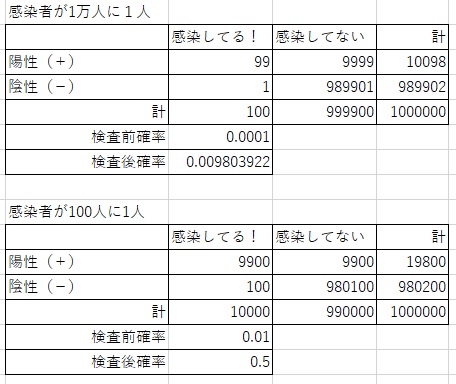
感染者が１万人に１人の方は、検査前確率が0.01％。検査後確率は0.98％。
つまり陽性だとしても本当に感染している可能性は1%未満という意味。

感染者が100人に１人としても、検査前確率は1%。検査後確率は50％。
これだけ感染が流行した状況で陽性が出ても、本当に感染している確率は五分五分。

検査対象を絞り込む

一番手っ取り早い解決策が、「感染していないかもしれない人」には、そもそも検査しない、という判断。
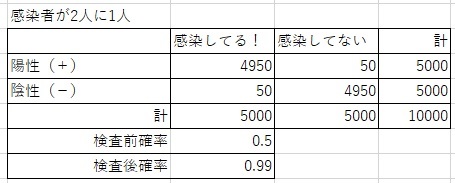
検査を行う前の診察の段階で「感染しているかどうか半々」つまり検査前確率を50%まで高めれば、

上図のように、検査後確率は99%という結果になった。

検査がダメ、という意図ではありません。その目的と、結果に対する正しい解釈が出来ていれば問題ないと思います。

以上。